Redraw of 4 Degree of Freedom Model

[dwsdolce]

I have reworked the 4 DOF model into SaberRD Student Edition. The model looks like the image below. It contains all of the elements that are in the equations in the book or in the Matlab/Octave model available on the Australian/New Zealand Luthiers forum. I get the same resonant frequencies with slightly different magnitude – I expect it is due to different numerical accuracy/order of equations in the two different solutions. This model does not require any of the equations in the book (beyond the differential equation). The simulator does the solution in the frequency domain and plots the results. If anyone cares to have the schematic and the model files I would be happy to send them to you. It is mostly a curiosity for me since the book does all the heavy lifting and the important parts are the sensitivities that Trevor calculated and documented in the book.
Regards
David

[Trevor Gore]

It would be interesting to see what happens if the body (sides) aren't "grounded" (line marked "reference" deleted) and the back stiffness (changed to a single Kb element) is connected directly to the sides (similar to how you have the top stiffness drawn). That would then be the same as the model I have, I think. Whether SaberRD will evaluate it then is a different matter!

[dwsdolce]

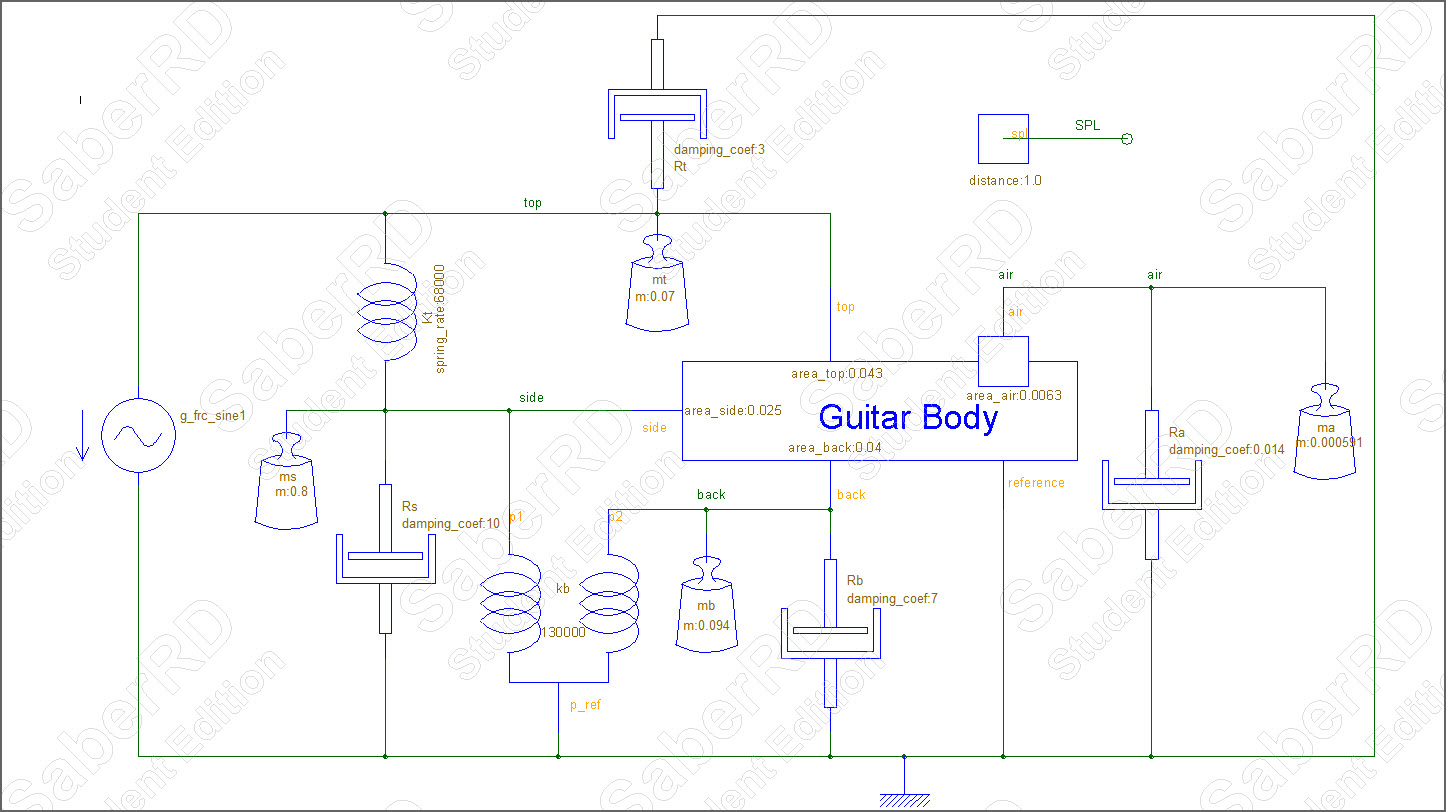
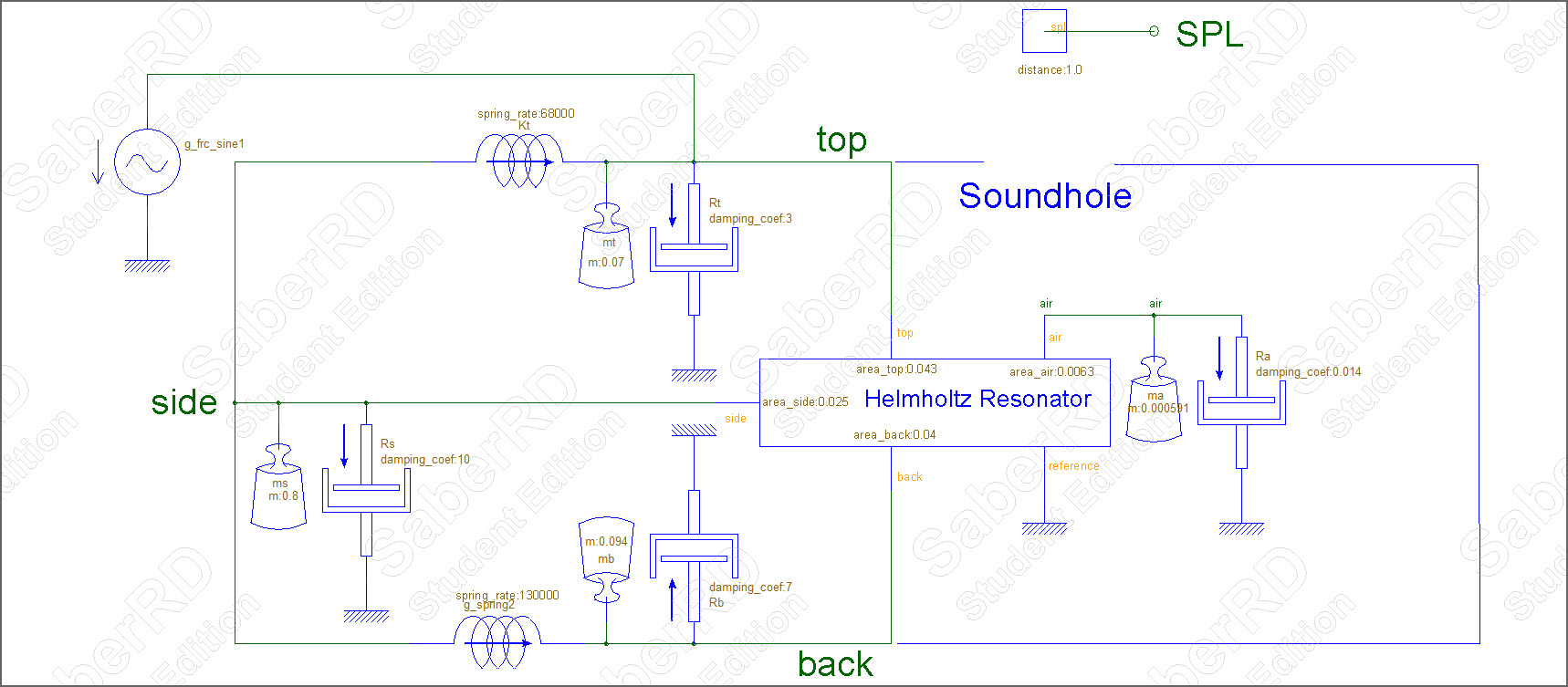
The DAE that this picture represents is identical to the model you have in the book. The back is not connected directly to the sides. There is a spring on the back whose force is equal to Kb times the sum of the motion of the back and sides and there is another spring on the sides whose force is equal to Kb times the sum of the motion of the back and sides. This is the core of the question that I was asking in the other post. The DAE in your book results in what is drawn. This is not limited to SaberRDS but it is a core principal of Mechatronic systems that a number of simulators support. It is based on the concept that physical systems can be modeled using acausal/conservative connection semantics where each element has a through and across variable at the connection. It holds for translational, rotational, thermal, pneumatic, hyrdraulic, electrical, magnetic etc...

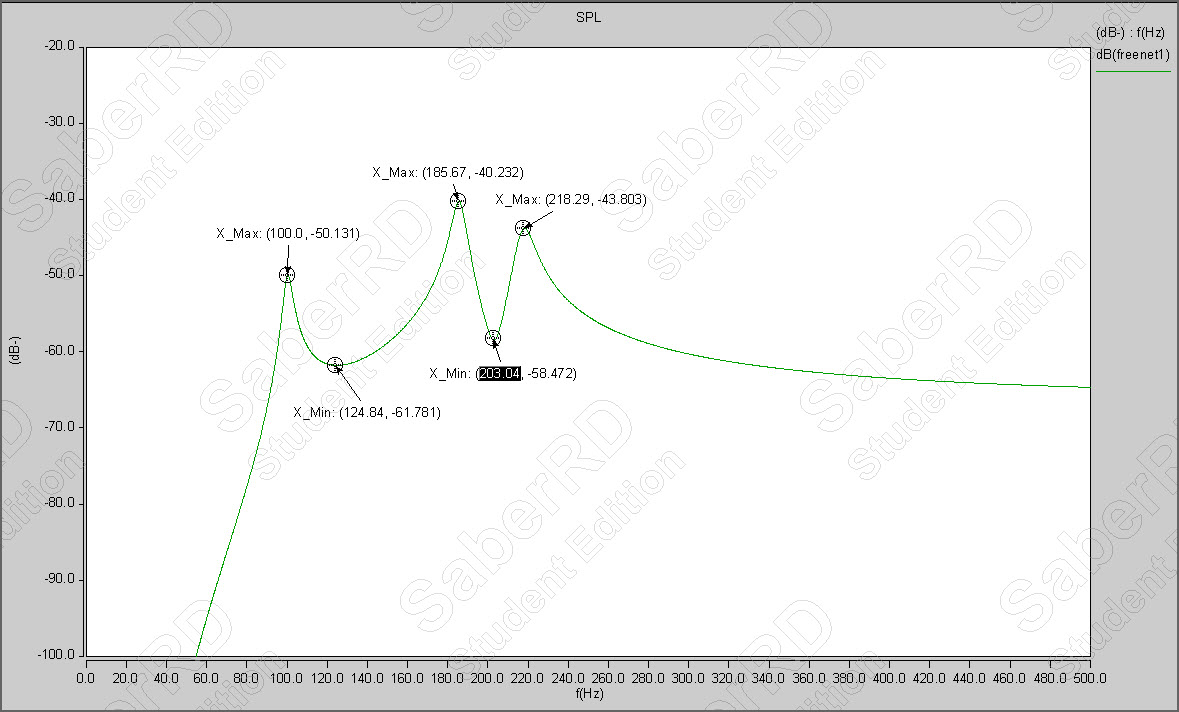
Another way to look at it is to ask the question: Is there any force applied to the back from the side or to the side from the back. In your equation there is not. If there were coupled then the term would be Kb(ys - yb) in the side equation and Kb(yb-ys) in the back equation. If they are stiffly connected then the easiest way to represent that would be to just sum the back and side mass. In addition, if they are connected then the back and sides would have the same motion. Running your model through Matlab/Octave and looking at the ys and yb terms shows that they do not have the same motion. They are not directly connected. The result of Matlab/Octave, using your solution of the DAE, agrees with the result of running this model in SaberRDS.

[Trevor Gore]

OK, some food for thought.

Another way to look at it is to ask the question: Is there any force applied to the back from the side or to the side from the back. In your equation there is not. If there were coupled then the term would be Kb(ys - yb) in the side equation and Kb(yb-ys) in the back equation.

If I'm understanding your model, it looks like you have all positive motion in the same direction. In the book model I have defined positive as outward from the guitar body. This may explain the sign difference. As we saw when I demonstrated the model in the class, coupling is happening. If not, when I changed the back stiffness (for example) it would not affect the other resonators, which it clearly did.

[dwsdolce]

I do not think the problem is in the model. The directions are all relative to ground. Consider that the ground is in the middle of the guitar and in that case all directions are positive in a direction from inside the body outward. That is how the equations are formed and the models within the equations. The equations for the Kb block are:
Force(side->reference) += Kb*(Position(back) + Position(side))
Force(back->reference) += Kb*(Position(back) + Position(side))

This means that the force contributed to the side is dependent on the displacement of the back and side and the force contributed to the back is dependent on the displacement of the back and side. This is exactly what your equations say. What I do not know is what the physical explanation of the relationship between the back and the sides is that results in this kind of coupling. It is not a spring coupling nor is it a mass coupling. It is a spring that is controlled by two different positions. Interesting. Anyway, the model seems to be correct since the equations that are formed by this are identical to the equations you have. And the results are consistent.

[Trevor Gore]

OK, David. Thanks for your insight.

[dwsdolce]

Hi Trevor,
First let me apologize. You were absolutely correct. The difference in my formulation was that I did not realize that the back difference and back pressure from the Helmholtz resonator needed to be inverted. I went back to the "Four mass coupled oscillator guitar model" article by John Popp in The Journal of the Acoustical Society of America 131, 829 (2012) and reread it a couple of times. Once I made the correction in the Helmholtz equations, this simplifies the model to a simple spring coupling between the top and side and the back and side. It turns out that the results of the simulation from the corrected model and the one that I had contrived were the same - but the formulation I did was a bit Rube-Goldberg-ish; which is why I was having trouble understanding it. Thanks for your perseverance. The model is now much simpler and I believe follows both your and Popp's intent.
.

[Trevor Gore]

Thanks for the update, David.

I downloaded SabreRD SE (all 1.5Gb!) so I could have a shot at some more exotic models. All I've got to do now is load it up and figure out how to use it (and find the time, which will likely be the most challenging thing!)

Thanks again.

[dwsdolce]

I am putting together a package for some of the people on Robbie's forum that includes the design, models, and some instructions to get started. I will send it to you once it is ready (Monday at the latest).

[Trevor Gore]

Thanks, David.